Scaling of Fourier transform in FFTW3
Fourier transformation in the FFTW3 library
The FFTW3 reference http://www.fftw.org/fftw3_doc/The-1d-Discrete-Fourier-Transform-_0028DFT_0029.html#The-1d-Discrete-Fourier-Transform-_0028DFT_0029 tells:
* 4.8.1 The 1d Discrete Fourier Transform (DFT)
*
* The forward (FFTW_FORWARD) discrete Fourier transform (DFT) of a 1d complex
* array X of size n computes an array Y, where:
*
* Y_k = sum_{j=0}^{n-1} X_j exp(-2i pi j k / n)
*
* The backward (FFTW_BACKWARD) DFT computes:
*
* X_k = sum_{j=0}^{n-1} Y_j exp(+2i pi j k / n)
*
* FFTW computes an unnormalized transform, in that there is no coefficient in
* front of the summation in the DFT. In other words, applying the forward and
* then the backward transform will multiply the input by n.
*
* From above, an FFTW_FORWARD transform corresponds to a sign of -1 in the
* exponent of the DFT. Note also that we use the standard in-order output
* orderingthe k-th output corresponds to the frequency k/n (or k/T, where T
* is your total sampling period). For those who like to think in terms of
* positive and negative frequencies, this means that the positive frequencies
* are stored in the first half of the output and the negative frequencies are
* stored in backwards order in the second half of the output. (The frequency
* -k/n is the same as the frequency (n-k)/n.)
* The forward transform is:
![\[ Y_k = \sum_{j=0}^{n-1} X_j e^{-i 2 \pi \frac{j k}{n}} \]](form_0.png)
The backward transform is:
![\[ X_k = \sum_{j=0}^{n-1} Y_j e^{i 2 \pi \frac{j k}{n}} \]](form_1.png)
Integral transform scaling
The Fourier transform presented here is scaled to represent the Fourier integral transform pair
![\[ \tilde{s}(\omega) = \int\limits_{-\infty}^{+\infty} s(t)\,e^{-i\omega t}\frac{\textrm{d}\omega}{2\pi} = \int\limits_{0}^{N\Delta t} s(t)\,e^{-i\omega t}\frac{\textrm{d}\omega}{2\pi} \]](form_2.png)
with 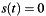 for
for 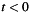 and
and 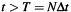 and
and
![\[ s(t) = \int\limits_{-\infty}^{+\infty} \tilde{s}(\omega)\,e^{i\omega t}\,\textrm{d}t = \int\limits_{-\pi/(N\Delta t)}^{+\pi/(N\Delta t)} \tilde{s}(\omega)\,e^{i\omega t}\,\textrm{d}t \]](form_6.png)
with 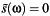 for
for 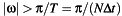 .
.
The FFTW3 transformation consequently has to be scaled according to
![\[ Y_k = \sum_{j=0}^{N-1} X_j e^{-i 2 \pi \frac{j k}{N}} \Delta t \]](form_9.png)
and
![\[ X_k = \sum_{j=0}^{N-1} Y_j e^{i 2 \pi \frac{j k}{N}} \frac{1}{N\Delta t} \]](form_10.png)
Where 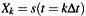 is the time series with
is the time series with 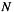 samples at
samples at 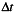 sampling interval.
sampling interval. 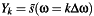 are samples of the Fourier integral transform, where
are samples of the Fourier integral transform, where 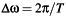 and
and 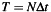 .
.
The library provides functions which return the appropriate scaling factors such that application of a inverse transformation in sequence with a forward transformation is an identity-operation.
